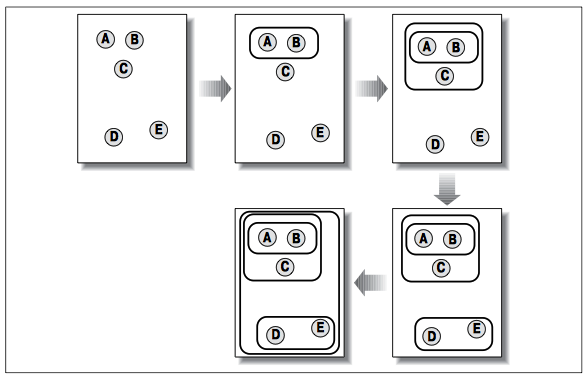
Он в корне отличается от иерархической кластеризации, поскольку ему нужно заранее указать, сколько кластеров генерировать. Алгоритм определяет размеры кластеров исходя из структуры данных.
Кластеризация методом K-средних начинается с выбора k случайно расположенных центроидов (точек, представляющих центр кластера). Каждому элементу назначается ближайший центроид. После того как назначение выполнено, каждый центроид перемещается в точку, рассчитываемую как среднее по всем приписанным к нему элементам. Затем назначение выполняется снова. Эта процедура повторяется до тех пор, пока назначения не прекратят изменяться.

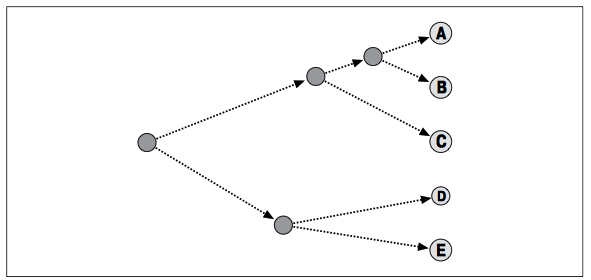
На первом шаге случайно размещены два центроида (изображены темными кружками). На втором шаге каждый элемент приписан к ближайшему центроиду. В данном случае A и B приписаны к верхнему центроиду, а C, D и E – к нижнему. На третьем шаге каждый центроид перемещен в точку, рассчитанную как среднее по всем приписанным к нему элементам. После пересчета назначений оказалось, что C теперь ближе к верхнему центроиду, а D и E – по-прежнему ближе к нижнему. Окончательный результат достигается, когда A, B и C помещены в один кластер, а D и E – в другой.
В данном методе, ОЧЕНЬ важен выбор центроидов, т.к. в конечном итоге все точки к ним стянутся, но если все 4 будут очень близкие цвета и из них будут состоять большие области, то в конечном итоге вы и получите приблизительно одинаковые центры. Таким образом центроиды должны быть максимально разнесены (желательно равномерно и равноудаленно).
Для большего понимания приведу пример. Давайте рассмотрим такую картинку.
Чтобы решить поставленную задачу в такой, монотонной четко разделенной картинке, достаточно написать небольшой код:
def k_cluster_by_area(points, k=4):
clusters_by_area = {}
for point in points:
clusters_by_area[point] = clusters_by_area.setdefault(point, 0) + 1
sorted_x = sorted(clusters_by_area.items(), key=operator.itemgetter(1))
return sorted_x[-k:]
Тут мы просто посчитали, сколько раз, какой цвет встречается, отсортировали и вывели k результатов. Этот метод можно применить к любому изображению, работает достаточно быстро, но есть НО! А именно, мы не получим ТОНАЛЬНОСТЬ картинки! Однако, как я писал выше, в нашей задаче важны центры, вот эту задачу и решает этот код!) Мы берем самые популярные цвета, за изначальные центры кластеров, а потом они постепенно мутируют) На самом деле, желательно брать не просто первые k, а посчитать все комбанации расстояний и выбрать k по макс расстояниям, чтобы центры не оказались рядом (например 2 оттенка серого). Но мне влом и вы сделаете это сами)
Надеюсь, стало яснее. Таким образом, как найти изначальные центры кластеров нам известно, осталось только свести все пиксели в эти точки. А теперь сам код:
def k_cluster(img, distance=euclidean, k=4):
points = get_points(img)
clusters = {}
# центры кластеры
cluster_centers = k_cluster_by_area(points, k)
for cluster_center in cluster_centers:
# avg_sum_coords - список сумм r, g, b координат всех пикселей кластера
# count_points - кол-во пикселей в кластере
# какие конкретно пиксели в кластере не запоминаем в целях экономии памяти и времени
clusters[cluster_center] = {'avg_sum_coords':list(cluster_center), 'count_points':1}
while len(points):
# находим ближайшие точки к центрам кластеров
bestmatches = {}
for point in points:
# расстояние каждой точки до каждого центра кластера
for cluster_center in clusters:
d = distance(cluster_center, point)
if not bestmatches:
bestmatches = {'distance':d, 'point': point, 'cluster_center': cluster_center}
if d < bestmatches['distance']:
bestmatches = {'distance': d, 'point': point, 'cluster_center': cluster_center}
# перекидываем ближайшие точки в соответствующий кластер
bestmatch = bestmatches['point']
cluster_center = bestmatches[
'cluster_center']
points2 = []
new_points = []
for point in points:
if point == bestmatch:
new_points.append(point)
else:
points2.append(point)
points = points2[:]
# меняем центр кластера
print clusters.keys(), len(points)
r_avg, g_avg, b_avg = 0, 0, 0
cluster_avg_coord = clusters[cluster_center]['avg_sum_coords']
new_points_len = len(new_points)
clusters[cluster_center]['count_points'] += new_points_len
claster_count_points = clusters[cluster_center]['count_points']
cluster_avg_coord[0] += bestmatch[0]*new_points_len
cluster_avg_coord[1] += bestmatch[1]*new_points_len
cluster_avg_coord[2] += bestmatch[2]*new_points_len
new_center = cluster_avg_coord[0]/claster_count_points, cluster_avg_coord[1]/claster_count_points, cluster_avg_coord[2]/claster_count_points
# если новый центр кластера отличается от предыдущего
if not new_center in clusters:
clusters[new_center] = clusters.pop(cluster_center)
return clusters.keys()
Работает это дело не быстро ;(, поэтому я советую сжимать картинку, хотя бы до разрешения 100 на 100.
Понятно, что идея не нова и сравнить вы можете, например с данным сайтом
http://design-seeds.comДавайте разберем пример. С указанного выше сайта взяли картинку и их разбиение на цвета. Здесь можно заметить, что их задача — это выбрать основные центровые цвета, что немного отличается от нашей задачи, но все же.
 |
| Пример с сайта |
Сначала посмотрим на наш метод выбора первоначальных центров, исходя из предположения простого количественного показателя использования цветов. Изначальные центры ниже подписано, сколько раз цвет встречался на картинке.
 |
| 7 раз |
 |
| 4 раза |
 |
| 4 раза |
 |
| 4 раза |
 |
| 5 раз |