Архив рубрики: Сортировки

Сортировка слиянием

Сортировка слиянием (англ. merge sort) — алгоритм сортировки, который упорядочивает списки (или другие структуры данных, доступ к элементам которых можно получать только последовательно, например — потоки) в определённом порядке. Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Наконец, их решения комбинируются, и получается решение исходной задачи. Алгоритм был изобретён Джоном фон Нейманом в 1945 году.

Странно, но мне показалось, что данный алгоритм не так сильно освещён в интернете в целом и на python  в частности. А ведь именно этот алгоритм чаще всего применяется для сортировки данных не помещающихся в оперативке, т.е. хранящихся в файлах(внешние сортировки). Как и в случае с быстрой сортировкой Хоара, существует 2 реализации данного алгоритма. Рекурсивная и нет) Скажу по секрету, не рекурсивную реализацию мне предоставил так же мой преподаватель Деон. Более того, она ещё и не требует дополнительной памяти, что в классическом варианте относят к её основным минусам!

Для решения задачи сортировки эти три этапа выглядят так:
  1. Сортируемый массив разбивается на две части примерно одинакового размера;
  2. Каждая из получившихся частей сортируется отдельно, например — тем же самым алгоритмом;
  3. Два упорядоченных массива половинного размера соединяются в один.
Рекурсивное разбиение задачи на меньшие происходит до тех пор, пока размер массива не достигнет единицы (любой массив длины 1 можно считать упорядоченным).
Нетривиальным этапом является соединение двух упорядоченных массивов в один. Основную идею слияния двух отсортированных массивов можно объяснить на следующем примере. Пусть мы имеем две стопки карт, лежащих рубашками вниз так, что в любой момент мы видим верхнюю карту в каждой из этих стопок. Пусть также, карты в каждой из этих стопок идут сверху вниз в неубывающем порядке. Как сделать из этих стопок од

Быстрая сортировка(quicksort, сортировка Хоара)

Быстрая сортировка (англ. quicksort), часто называемая qsort по имени реализации в стандартной библиотеке языка Си — широко известный алгоритм сортировки, разработанный английским информатиком Чарльзом Хоаром в 1960 году. Один из быстрых известных универсальных алгоритмов сортировки массивов (в среднем O(n log n) обменов при упорядочении n элементов), хотя и имеющий ряд недостатков. Например, в худшем случае (на некоторых входных массивах) использует время Ω(n2), что, например, хуже, чем сложность в наихудшем случае алгоритма сортировки слиянием. 

Функция QuickSort сводит сортировку данного ей массива к разделению (partitioning) этого массива на две группы элементов и сортировке этих двух групп по отдельности.


Пример рекурсивного алгоритма с детерменированным(определённым) выбором оси:

Пусть нам нужно отсортировать участок массива A с p-го по q-й элемент включительно, будем называть этот участок подмассивом и обозначать как A[p..q].

  • ШАГ 1: Возьмем элемент A[p] за ось и «раскидаем» остальные элементы A[(p+1)..q] по разные стороны от него стороны — меньшие влево, большие — вправо, то есть переставим элементы подмассива A[p..q] так, чтобы вначале шли элементы меньше либо равные A[p] потом элементы, больше либо равные A[p]. Назовет этот шаг разделением (partition).

  • ШАГ 2: Пусть r есть новый индекс элемента A[p]. Тогда, если q — p > 2, вызовем функцию сортировки для подмассивов A[p..(r-1)] и A[(r+1)..q].

Ключевая идея алгоритма заключается в процедуре «partition», которая за линейное время от размера массива, осуществляет такую перестановку элементов, относительно некоторой «оси» — заданного значения, равного одному из значений сортируемого интервала массива, что переставленный массив состоит из трех интервалов, идущих по порядку:

  1. Элементы меньшие «оси»
  2. Элементы равные «оси»
  3. Элемент

Пузырьковая сортировка

Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При проходе алгоритма, элемент, стоящий не на своём месте, «всплывает» до нужной позиции как пузырёк в воде, отсюда и название алгоритма.
Для понимания и реализации этот алгоритм — простейший, но эффективен он лишь для небольших массивов. Сложность алгоритма: O(n²).
*-Нравится статья? Кликни по рекламе! 🙂

Расположим массив сверху вниз, от нулевого элемента — к последнему.

Идея метода: шаг сортировки состоит в проходе снизу вверх по массиву. По пути просматриваются пары соседних элементов. Если элементы некоторой пары находятся в неправильном порядке, то меняем их местами.

После нулевого прохода по массиву «вверху» оказывается самый «легкий» элемент — отсюда аналогия с пузырьком. Следующий проход делается до второго сверху элемента, таким образом второй по величине элемент поднимается на правильную позицию.

Делаем проходы по все уменьшающейся нижней части массива до тех пор, пока в ней не останется только один элемент. На этом сортировка заканчивается, так как последовательность упорядочена по возрастанию.




Среднее число сравнений и обменов имеют квадратичный порядок роста: O(n2), отсюда можно заключить, что алгоритм пузырька очень медленен и малоэффективен.
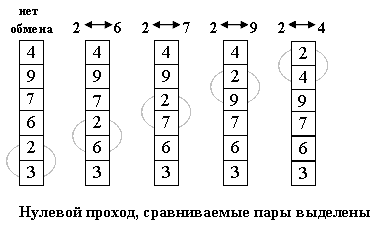
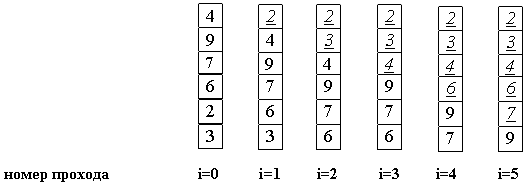
Тем не менее, у него есть громадный плюс: он прост и его можно по-всякому улучшать. 
Чем мы сейчас и займемся:
  1. Во-первых, рассмотрим ситуацию, когда на каком-либо из проходов не произошло ни одного обмена. Что это значит ?Это значит, что все пары расположены в правильном порядке, так что массив уже отсортирован. И продолжать процесс не имеет смысла(особенно, если массив был отсортирован с самого начала !).Итак, первое улучшение алгоритма заключается в запоминании, производился ли на данном проходе какой-либо обмен. Если нет — алгоритм заканчивает работу.
  2. Процесс улучшения можно продолжить, если запоминать не только сам факт обмена, но и индекс последнего обмена k. Действительно: все пары соседих элементов с индексами, меньшими k, уж