Пузырьковая сортировка

Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При проходе алгоритма, элемент, стоящий не на своём месте, «всплывает» до нужной позиции как пузырёк в воде, отсюда и название алгоритма.
Для понимания и реализации этот алгоритм — простейший, но эффективен он лишь для небольших массивов. Сложность алгоритма: O(n²).
*-Нравится статья? Кликни по рекламе! 🙂

Расположим массив сверху вниз, от нулевого элемента — к последнему.

Идея метода: шаг сортировки состоит в проходе снизу вверх по массиву. По пути просматриваются пары соседних элементов. Если элементы некоторой пары находятся в неправильном порядке, то меняем их местами.

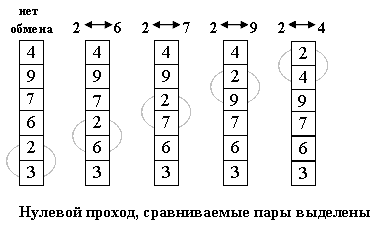
После нулевого прохода по массиву «вверху» оказывается самый «легкий» элемент — отсюда аналогия с пузырьком. Следующий проход делается до второго сверху элемента, таким образом второй по величине элемент поднимается на правильную позицию.

Делаем проходы по все уменьшающейся нижней части массива до тех пор, пока в ней не останется только один элемент. На этом сортировка заканчивается, так как последовательность упорядочена по возрастанию.




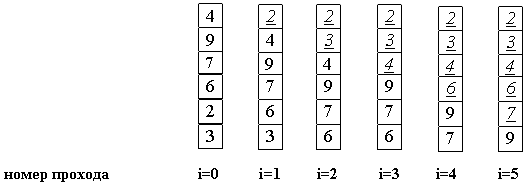
Среднее число сравнений и обменов имеют квадратичный порядок роста: O(n2), отсюда можно заключить, что алгоритм пузырька очень медленен и малоэффективен.
Тем не менее, у него есть громадный плюс: он прост и его можно по-всякому улучшать. 
Чем мы сейчас и займемся:
  1. Во-первых, рассмотрим ситуацию, когда на каком-либо из проходов не произошло ни одного обмена. Что это значит ?Это значит, что все пары расположены в правильном порядке, так что массив уже отсортирован. И продолжать процесс не имеет смысла(особенно, если массив был отсортирован с самого начала !).Итак, первое улучшение алгоритма заключается в запоминании, производился ли на данном проходе какой-либо обмен. Если нет — алгоритм заканчивает работу.
  2. Процесс улучшения можно продолжить, если запоминать не только сам факт обмена, но и индекс последнего обмена k. Действительно: все пары соседих элементов с индексами, меньшими k, уж