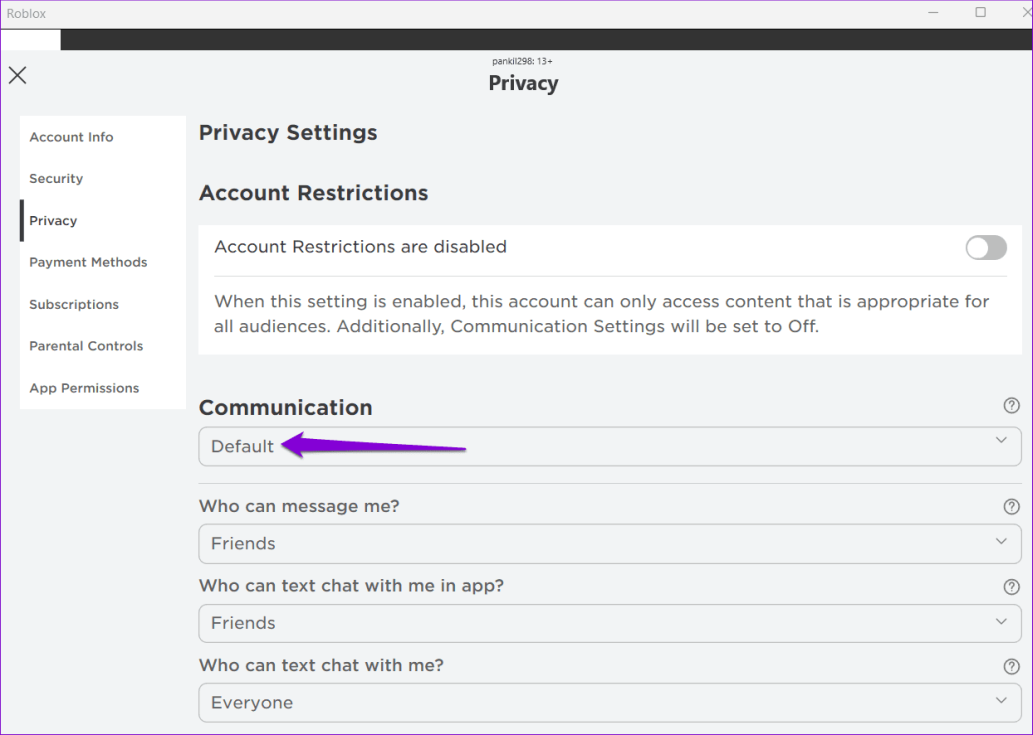
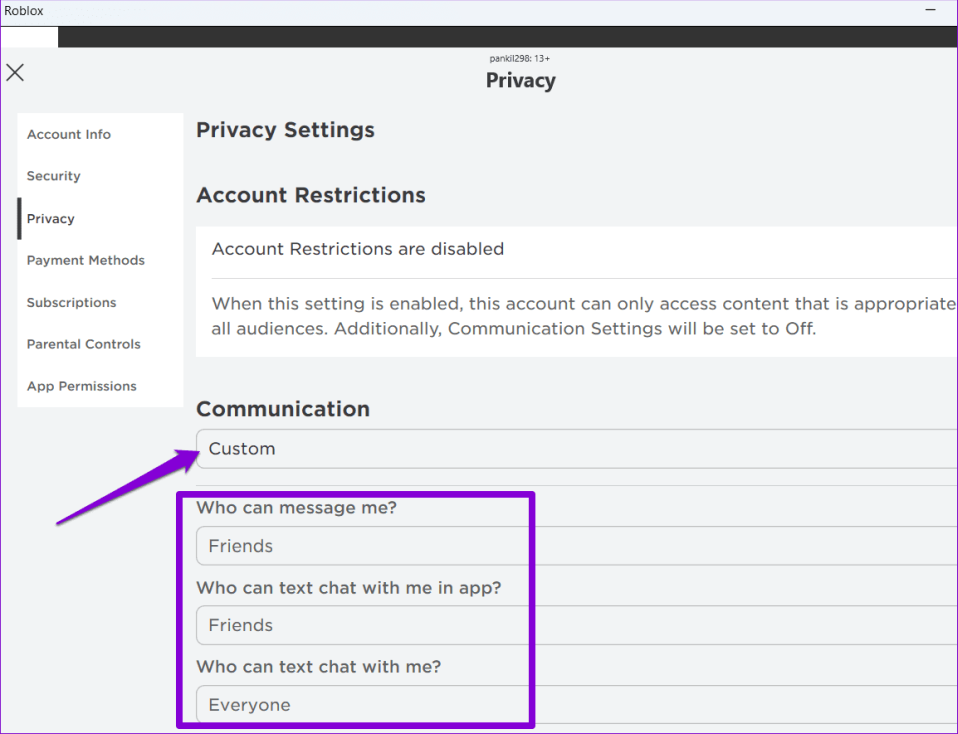
В мире информатики и программирования структуры данных играют фундаментальную роль в эффективной организации данных и манипулировании ими. Одной из таких важных структур данных является Карта. Карта, также известная как ассоциативный массив, словарь или таблица символов, обеспечивает мощную абстракцию, которая позволяет хранить и извлекать данные в формате пары ключ-значение. В этой статье мы рассмотрим структуру данных карты, ее характеристики и области применения.
Карта структуры данных
Карта — это контейнер для элементов, которые хранятся в виде комбинации ключей и соответствующих значений. Карты, в отличие от массивов или списков, используют уникальные ключи для идентификации связанных с ними значений и доступа к ним. Это обеспечивает быстрый поиск и модификацию данных без необходимости знать конкретный индекс или местоположение.
Ключевые особенности карты структуры данных
1. Сопряжение ключ-значение: Сопряжение ключ-значение является фундаментальной концепцией структуры данных карты. Каждый элемент карты состоит из уникального ключа и соответствующего ему значения.
2. Быстрый доступ: Карты обеспечивают эффективные операции поиска на основе ключа. Используя базовую структуру данных, такую как сбалансированное бинарное дерево поиска или хэш-таблицу, карты могут достигать постоянной или логарифмической временной сложности для обычных операций.
3. Динамический размер: Карты могут динамически увеличиваться и уменьшаться в размерах по мере добавления или удаления элементов. Такая гибкость делает их пригодными для обработки различных объемов данных.
4. Уникальность ключей: Каждый ключ на карте должен быть уникальным. Повторяющиеся ключи не допускаются, гарантируя, что каждая пара ключ-значение представляет отдельную запись.
Типы карт в структурах данных
В информатике и структурах данных существует несколько типов карт или словарных структур данных:
1. Хэш-карта
Хэш-карта — это структура данных, которая сопоставляет ключи с индексами массива с помощью хэш-функции. Хэш-функция принимает ключ в качестве входных данных и возвращает индекс в массив, содержащий соответствующее значение. Хэш-карты — одна из наиболее эффективных структур данных карты, со средней временной сложностью O (1) для таких операций, как вставка и извлечение. Коллизии хэшей могут возникать, когда два ключа сопоставляются с одним и тем же индексом, что приводит к снижению производительности в наихудшем сценарии.
2. Древовидная карта
Древовидная карта — это тип карты, который использует бинарное дерево поиска в качестве своей реализации. Ключи в древовидной карте хранятся в отсортированном порядке, что позволяет выполнять эффективные операции поиска, вставки и удаления. Для таких операций, как вставка и извлечение, древовидные карты имеют среднюю временную сложность O (log n), где n — количество элементов на карте.
3. Связанная хэш-карта
Связанная хэш-карта — это тип карты, который хранит двусвязный список элементов карты в том порядке, в котором они были вставлены. Это обеспечивает быструю итерацию элементов карты, а также эффективные операции вставки, извлечения и удаления.
4. Трехмерная карта
Трехуровневая карта, также известная как дерево префиксов, представляет собой тип карты, используемый для хранения набора строк, где каждый узел представляет собой префикс одной или нескольких строк. Попытки особенно полезны для поиска строк, начинающихся с определенного префикса, потому что поиск может быть остановлен раньше, если префикс не найден в дереве.
5. Карта фильтров Блума
Карта с фильтром блума — это карта, которая использует фильтр Блума, вероятностную структуру данных, для определения того, существует ли ключ на карте. Карты с фильтром Блума используются, когда требуется быстрое время отклика для проверки наличия ключа, но иногда допустим ложноположительный результат.
Структура данных карты на разных языках
1. Карты в C ++
Карты — это ассоциативные контейнеры, которые отображают элементы для хранения. Каждый элемент имеет сопоставленное значение и ключевое значение. Никакие два сопоставленных значения не могут иметь одинаковые ключевые значения.
Типы карт в C ++:
- Order Map
- Unordered_map
- Multi map
Синтаксис:
Order Map - mapmp
Unordered Map - unordered_mapmp
Multi map - multimapmp
2. Карты на Java
Java включает в себя интерфейс map. Сопоставление между ключом и значением представлено пакетом util. Интерфейс Map не является подтипом интерфейса Collection. Поэтому он ведет себя немного иначе, чем остальные типы коллекций.
Типы карт в Java:
- HashMap
- Linked Hash Map
- Tree Map
Синтаксис:
HashMap - Map map = new HashMap<>();
Linked Hash Map - Map map = new LinkedHashMap<>();
Tree Map - Map map = new TreeMap<>();
3. Карты в Python
Функция map() возвращает объект map (итератор) результатов применения данной функции к каждому элементу итерации (списку, кортежу и т.д.).
Синтаксис:
map(fun, iter)
Внутренняя реализация карты структуры данных
Карта структуры данных состоит из пар ключ-значение, которые обеспечивают быстрый доступ к значениям на основе соответствующих ключей. Внутренняя реализация структуры данных карты определяется используемым языком программирования или библиотекой.
Карта структуры данных обычно реализуется в виде ассоциативного массива или хэш-таблицы, где каждой паре ключ-значение присваивается уникальный индекс с помощью хэш-функции. Значение, связанное с этим ключом, затем сохраняется и извлекается с использованием этого индекса.
Карта структуры данных
Когда к карте добавляется новая пара ключ-значение, хэш-функция используется для вычисления индекса ключа, и значение сохраняется по этому индексу. Если значение уже сохранено по этому индексу, новое значение заменяет старое.
Упорядоченная или неупорядоченная карта
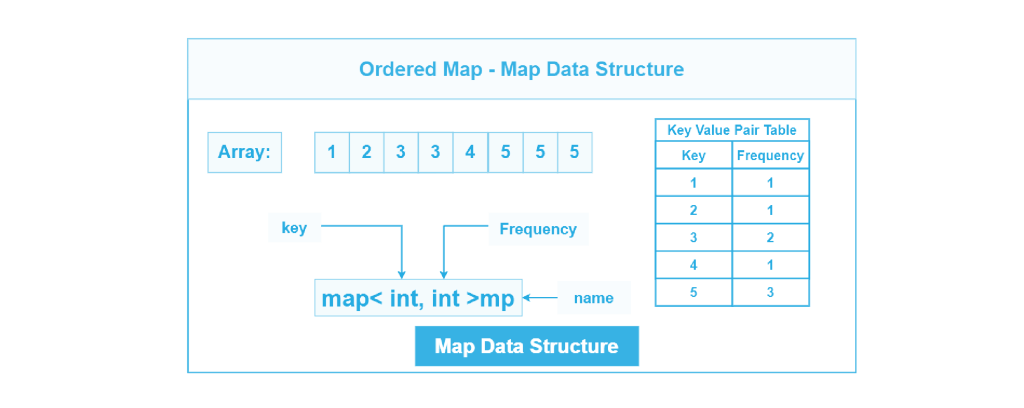
Упорядоченная карта
Упорядоченная карта реализована на C ++ с использованием контейнера std::map из стандартной библиотеки шаблонов (STL). Шаблонный контейнер std:: map хранит пары ключ-значение в отсортированном порядке в соответствии с ключами.

Реализация упорядоченной карты на C ++
#include
using namespace std;
void countFreq(int arr[], int n)
{
map mp;
for (int i = 0; i < n; i++)
mp[arr[i]]++;
for (auto x : mp)
cout << x.first << " " << x.second << endl;
}
int main()
{
int arr[] = { 1, 2, 3, 3, 4, 5, 5, 5 };
int n = sizeof(arr) / sizeof(arr[0]);
countFreq(arr, n);
return 0;
}
import java.io.*;
import java.util.*;
class Prepbytes {
static void countFreq(int[] arr, int n)
{
Map mp = new HashMap();
for (int i = 0; i < n; i++)
mp.put(arr[i], mp.getOrDefault(arr[i], 0) + 1);
for (Map.Entry entry :
mp.entrySet())
System.out.println(entry.getKey() + " "
+ entry.getValue());
}
public static void main(String[] args)
{
int[] arr = { 1, 2, 3, 3, 4, 5, 5, 5 };
int n = arr.length;
countFreq(arr, n);
}
}
from collections import defaultdict
def countFreq(arr):
freq = defaultdict(int)
for i in arr:
freq[i] += 1
for key, value in freq.items():
print(key, value)
if __name__ == "__main__":
arr = [1, 2, 3, 3, 4, 5, 5, 5]
countFreq(arr)
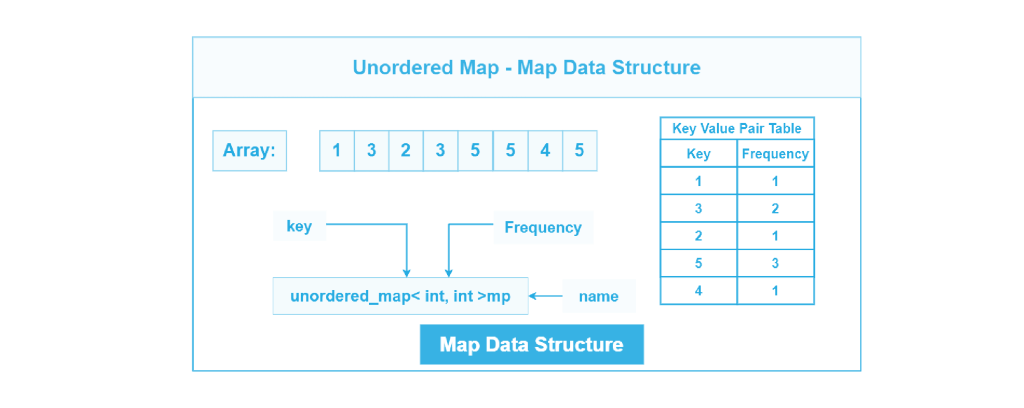
Неупорядоченная карта
Неупорядоченная карта реализована в C ++ с помощью контейнера std::unordered_map из стандартной библиотеки шаблонов (STL). Шаблонный контейнер std::unordered_map хранит пары ключ-значение неупорядоченным образом на основе хэш-значений ключей.

Операции, связанные с картами структуры данных
Карта — это структура данных, в которой хранятся пары ключ-значение. Вот некоторые из наиболее распространенных операций, которые вы можете выполнять с картой:
- Вставка: Мы можем добавить новую пару ключ-значение на карту и присвоить ей значение.
- Извлечение: мы можем получить значение, связанное с ключом, и передать ключ в качестве аргумента.
- Обновление: Мы можем обновить значение, связанное с ключом, и присвоить ключу новое значение.
- Удалить: Используя метод erase() и ключ в качестве аргумента, мы можем удалить пару ключ-значение с карты.
- Поиск: Мы можем использовать метод count (), чтобы увидеть, существует ли ключ на карте, или мы можем проверить, равно ли значение, связанное с ключом, значению по умолчанию.
- Итерация: мы можем выполнять итерации по парам ключ-значение на карте, используя цикл for или итератор.
- Сортировка: В зависимости от того, как реализована карта, мы можем сортировать пары ключ-значение либо по ключам, либо по значениям.
Свойства карты структуры данных
Вот некоторые свойства карты структуры данных:
- Все ключи на карте уникальны, что означает, что каждый ключ может соответствовать только одному значению.
- Карты изменяемы, что означает, что их элементы могут быть изменены после их создания.
- Карты связывают ключи со значениями, что означает, что каждый ключ связан ровно с одним значением.
- Упорядоченность: Картам не присуща упорядоченность, что означает, что порядок, в котором элементы вставляются в карту, не имеет отношения к порядку, в котором они извлекаются.
- Хэширование: Хэш-таблицы обычно используются для реализации карт, что означает, что ключи хэшируются с индексами в базовом массиве, а значения хранятся в соответствующих элементах массива.
- Сложность: Временная сложность основных операций с картой, таких как вставка, поиск и удаление, обычно составляет в среднем O (1), что означает, что эти операции занимают одинаковое количество времени независимо от размера карты. Однако в случае коллизий хэшей временная сложность в наихудшем случае может составлять O (n), где n — количество элементов на карте.
Приложения карты структуры данных
Карты структуры данных находит применение в различных областях и сценариях, включая:
- Словарь: Карты обычно используются для реализации словарей, где слова (ключи) связаны с их определениями (значениями). Это обеспечивает эффективный поиск слов.
- Кэширование: Карты могут использоваться в системах кэширования для хранения часто используемых данных. Ключи представляют собой уникальные идентификаторы, а значения хранят соответствующие кэшированные данные. Это помогает повысить производительность за счет уменьшения необходимости в дорогостоящих операциях.
- Таблицы символов: Компиляторы и интерпретаторы широко используют карты для построения таблиц символов, связывая идентификаторы (ключи) с соответствующими переменными или функциями (значениями).
- Индексация базы данных: Карты играют решающую роль в структурах индексации базы данных, таких как B-деревья и хэш-индексы. Они обеспечивают эффективный поиск и извлечение записей на основе определенных ключей.
Заключение
Карта структуры данных предоставляет мощный и гибкий способ хранения данных и доступа к ним на основе уникальных ключей. Ее сопряжение ключ-значение и эффективные операции поиска делают ее ценным инструментом в различных приложениях, включая словари, системы кэширования, таблицы символов и индексацию баз данных. Понимание структуры данных карты и ее возможностей позволяет программистам разрабатывать эффективные алгоритмы и с легкостью обрабатывать данные.
Часто задаваемые вопросы (FAQs)
Вопрос 1. В чем разница между картой и массивом?
В отличие от массивов, которые используют целочисленные индексы для доступа к элементам, карты используют уникальные ключи для хранения и извлечения значений. Карты обеспечивают более гибкий и эффективный способ организации данных, поскольку они позволяют осуществлять быстрый поиск и модификации на основе ключей, независимо от их расположения или порядка.
Вопрос 2. Может ли карта содержать дубликаты ключей?
Нет, карты не допускают дублирования ключей. Каждый ключ должен быть уникальным на карте. Если вы попытаетесь вставить пару ключ-значение с уже существующим ключом, это либо заменит существующее значение, либо отклонит вставку, в зависимости от реализации и языка программирования.
Вопрос 3. Как карта обрабатывает вставку пары ключ-значение?
При вставке пары ключ-значение в карту внутренняя реализация карты гарантирует, что ключ хранится таким образом, который обеспечивает эффективный поиск. Конкретный механизм может варьироваться в зависимости от реализации, например, при использовании сбалансированного бинарного дерева поиска или хэш-таблицы.
Вопрос 4. Какова временная сложность доступа к элементам карты?
Временная сложность доступа к элементам карты зависит от базовой реализации. В большинстве случаев она либо постоянная (O(1)), либо логарифмическая (O(log n)), где n представляет количество элементов на карте. Такая эффективность обеспечивает быстрый доступ и извлечение данных даже для больших карт.
Вопрос 5. Могу ли я изменить значение, связанное с ключом на карте?
Да, карты предоставляют методы для обновления значения, связанного с определенным ключом. Вы можете изменить значение, обратившись к нему через соответствующий ключ и присвоив новое значение. Карта автоматически обновит значение и сохранит связь ключ-значение.
2024-01-08T13:14:07
Программирование