Рассмотрим математическую модель, используемую для управления
светофорами на сложном перекрестке дорог. Мы должны создать программу, которая в
качестве входных данных использует множество всех допустимых поворотов на перекрестке (продолжение прямой дороги, проходящей через перекресток, также будем
считать «поворотом») и разбивает это множество на несколько групп так, чтобы все повороты в группе могли выполняться одновременно, не создавая проблем друг для друга. Затем мы сопоставим с каждой группой поворотов соответствующий режим работы
светофоров на перекрестке.

*-Нравится статья? Кликни по рекламе! 🙂

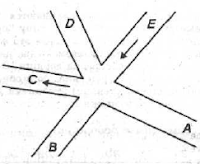Рис. 1.1. Сложный перекресток

Желательно минимизировать число разбиений исходного множества поворотов, поскольку при этом минимизируется количество режимов работы светофоров на перекрестке.
Для примера на рис. 1.1 показан перекресток возле Принстонского университета, известный сложностью его преодоления. Обратите внимание, что дороги С и E односторонние, остальные — двухсторонние. Всего на этом перекрестке возможно 13 поворотов. Некоторые-из этих поворотов, такие как АВ (поворот с дороги А на дорогу В) и ЕС, могут выполняться одновременно. Трассы других поворотов, например АО и ЕВ, пересекаются, поэтому их нельзя выполнять одновременно. Режимы работы светофоров должны учитывать эти обстоятельства.

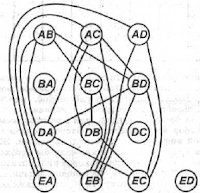Рис. 1.2. Граф, показывающий несо- вместимые повороты

Для построения модели этой задачи можно применить математическую структуру, известную как граф. Для решения задачи можно нарисовать граф, где вершины будут представлять повороты, а ребра соединят ту часть вершин-поворотов, которые нельзя выполнить одновременно. Для нашего перекрестка соответствующий граф показан на рис. 1.2, а в табл. 1.1 дано другое представление графа — в виде таблицы(матрицы смежности), где на пересечении строки i и столбца j стоит 1 тогда и только тогда, когда существует ребро между вершинами i и j.

Таблица 1.1. Таблица несовмести